خوارزميات البحث المستنيرة | الوحدة الثانية | الدرس الرابع

خوارزميات البحث المستنيرة هو عنوان الدرس الرابع من الوحدة الثانية التي تحمل اسم “خوارزميات الذكاء الاصطناعي” من الفصل الدراسي الأول من مقرر “الذكاء الاصطناعي”.

ستتعرف في هذا الموضوع على كيفية تحديد بعض الأمثلة على خوارزميات البحث، والتمييز بين أنواعها، وكيفية إنشاء ألغاز المتاهة بواسطة البايثون، وكيفية استخدام خوارزمية البحث بأولوية الاتساع في حل ألغاز المتاهة، بالإضافة لاستخدام خوارزمية البحث بأولوية الأفضل في حل ألغاز المتاهة.

لذا قم بقراءة أهداف التعلُّم بعناية، ثم أعد قراءتها وتأكَّد من تحصيل كافة محتوياتها بعد انتهائك من دراسة الموضوع.

أهداف التعلُّم

• تحديد بعض الأمثلة على خوارزميات البحث.
• التمييز بين أنواع خوارزميات البحث.
• إنشاء ألغاز المتاهة بواسطة البايثون.
• استخدام خوارزمية البحث بأولوية الاتساع في حل ألغاز المتاهة.
• استخدام خوارزمية البحث بأولوية الأفضل في حل ألغاز المتاهة.
• المقارنة بين خوارزميات البحث.

هيا لنبدأ!

تطبيقات خوارزميات البحث (Applications of Search Algorithms)

خوارزميات البحث هي الأكثر أحد المكونات الرئيسة لأنظمة الذكاء الاصطناعي، فباستخدامها يمكن اكتشاف الاحتمالات المختلفة لإيجاد الحلول المناسبة للمشكلات المعقدة في العديد من التطبيقات السائدة وفيما يلي أمثلة على بعض تطبيقات خوارزميات البحث:

• الروبوتية (Robotics)

يستخدم الروبوت خوارزمية البحث لتحديد طريقة عبر المتاهة أو لتحديد موقع أحد الكائنات في نطاق بيئته.

• مواقع التجارة الالكترونية (E-commerce Websites)

تستخدم مواقع التسويق عبر الإنترنت خوارزميات البحث لتطابق بين استفسارات العملاء وبين المنتجات المتوفرة.

لتصفية نتائج البحث وفق بعض المعايير مثل: السعر، العلامة التجارية، التقييمات واقتراح المنتجات ذات الصلة.

• منصات مواقع التواصل الاجتماعي (Social Media Platforms)

تستخدم مواقع التواصل الاجتماعي خوارزميات البحث لعرض التدوينات، والأشخاص الروبوت والمجموعات للمستخدمين وفقًا للكلمات المفتاحية واهتمامات المستخدم.

• تمكين الآلة من ممارسة الألعاب بمستوى عالٍ من المهارة (Enabling a machine to play games at high skill level)

يستخدم الذكاء الاصطناعي خوارزمية البحث أثناء لعب الشطرنج أو قو (Go) لتقييم الحركات المختلفة واختيار الخطوات التي من المرجح أن تؤدي إلى الفوز الحالة الأولية.

• نظم الملاحة باستخدام محدد المواقع العالمي (GPS Navigation System)

تستخدم نظم الملاحة القائمة على محدد المواقع العالمي خوارزميات البحث لتحديد أقصر وأسرع طريق بين موقعين مع مراعاة بيانات حركة المرور في الوقت الحالي.

• نظم إدارة الملفات (File Management System)

تستخدم خوارزميات البحث في نظم إدارة الملفات لتحديد موقع الملفات باستخدام اسم ومحتوى الملفات وبعض السمات الأخرى.

أنواع خوارزميات البحث وأمثلتها (Types and Examples of Search Algorithms)

هناك نوعان رئيسان من خوارزميات البحث وهما:

• خوارزميات البحث غير المستنيرة (Uninformed Search Algorithm)
• خوارزميات البحث المستنيرة (Informed Search Algorithm)

 

خوارزميات البحث غير المستنيرة (Uniformed Search Algorithm)

تسمى أيضًا (خوارزميات البحث العمياء)، هي تلك التي لا تحتوي على معلومات إضافية حول حالات المشكلة باستثناء المعلومات المستفادة من تعريف المشكلة.

تقوم هذه الخوارزميات بإجراء فحص شامل لمساحة البحث استنادًا إلى مجموعة من القواعد المحددة مسبقًا.

أمثلة على خوارزميات البحث غير المستنيرة:

• خوارزمية البحث بأولوية الاتساع (BFS).
• خوارزمية البحث بأولوية العمق (DFS).

لمعرفة المزيد من المعلومات عن خوارزمية البحث غير المستنيرة، ثم بالاطّلاع على الرابط التالي:

على سبيل المثال، تبدأ خوارزمية البحث بأولوية العمق (DFS) عند عقدة الجذر بالشجرة أو المخطط وتتوسع حتى تصل للعقدة الأعمق التي لم تفحص ويستمر الأمر بهذه الطريقة حتى تستنفذ الخوارزمية مساحة البحث بأكملها بعد فحص كل العقد المتاحة، ثم تُخرج الحل الأمثل الذي وجدته أثناء البحث. فالحقيقة أن خوارزمية البحث بأولوية العمق (DFS) يتبع دومًا هذه القواعد ولا يمكن ضبط استراتيجيتها بصرف النظر عن نتائج البحث وهذا ما يجعلها خوارزمية غير مستنيرة.

ومثال آخر, ملحوظ على هذا النوع من الخوارزميات هو خوارزمية البحث بأولوية العمق التكراري المتعمق (Iterative Deeping Depth-First Search – IDDFS) التي يمكن اعتبارها مزيجًا بين خوارزميتي البحث بأولوية العمق (DFS) والبحث بأولوية الاتساع (BFS)، فهي تستخدم استراتيجية العمق أولاً للبحث في جميع الخيارات الموجودة في النطاق الكامل بصورة متكررة حتى تصل إلى عقدة محددة.

خوارزميات البحث المستنيرة (Informed Search Algorithm)

على النقيض من خوارزميات البحث غير المستنيرة.

تَستخدِم خوارزميات البحث المستنيرة المعلومات حول المشكلة ومساحة البحث لتوجيه عملية البحث.

أمثلة على خوارزميات البحث المستنيرة:

• خوارزمية البحث بأولوية الأفضل (A*search)

تستخدم دالة استدلالية لتقدير المسافة بين كل عقدة من العقد المرشحة والعقدة المستهدفة. ثم توسع العقدة المرشحة بالتقدير الأقل.

إن فعالية خوارزمية البحث بأولوية الأفضل A*Search مرتبطة بجودة دالتها الاستدلالية. على سبيل المثال، إذا كنت تضمن أن الاستدلال لن يتجاوز المسافة الفعلية إلى الهدف، فبالتالي سوف تعثر الخوارزمية على الحل الأمثل بخلاف ذلك، قد لا يكون الحل الناتج من الخوارزمية هو الأفضل.

لمعرفة المزيد من المعلومات عن خوارزمية البحث بأولوية الأفضل، قم بالاطّلاع على الرابط التالي:

خوارزمية البحث بأولوية الأفضل – ويكيبيديا

تعريف هام

الدالة الاستدلالية (Heuristic Function)

هي الدالة التي تُصنِّف البدائل في خوارزميات البحث عند كل مرحلة فرعية استنادًا إلى تقديرات استدلالية مبنية على البيانات المتوفرة لتحديد الفَرع الذي ستسلكه.

• خوارزمية ديكسترا (Dijkstra Algorithm)

توسع العقدة بناء على أقصر مسافة فعلية إلى الهدف في كل خطوة، ولذلك على النقيض من خوارزمية البحث بأولوية الأفضل.

تحسب خوارزمية ديكسترا المسافة الفعلية ولا تستخدم التقديرات الاستدلالية وبينما يجعل هذا خوارزمية ديكسترا أبطأ من خوارزمية البحث بأولوية الأفضل إلا أن ذلك يعني ضمان العثور على الحل الأمثل دومًا ممثلاً بالمسار ألأقصر من البداية حتى الهدف.

• خوارزمية تسلق التلال (Hill Climbing)

تبدأ بتوليد حل عشوائي، ثم تحاول تحسين هذا الحل بصورة متكررة بإجراء تغييرات بسيطة تحسن من دالة استدلالية محددة وبالرغم من أن هذه المنهجية لا تضمن إيجاد الحل الأمثل، إلا أنها سهلة التنفيذ وتتميز بفعالية كبيرة عند تطبيقها على أنواع معينة من المشكلات.

لاحظ أن

الخلايا ذات اللون البنفسجي هي الخلايا التي تمّ فحصها، والخلية ذات اللون الأخضر هي موضع البدء، والخلية ذات اللون الأحمر هي موقع الهدف، بينما الخلايا ذات اللون الأصفر تمثل المسار الذي تم العثور عليه.

تطبيقات خوارزمية البحث Applications of search algorithm

في هذه الوحدة، ستشاهد بعض الأمثلة المرئية وتطبيقات البايثون على خوارزمية البحث بأولوية الاتساع (BFS)وخوارزمية البحث بأولوية الأفضل (a*search) لمعرفة الاختلافات بين خوارزميتي البحث المستنيرة وغير المستنيرة.

إنشاء ألغاز المتاهة بواسطة البايثون (Creating Maze Puzzles in Python)

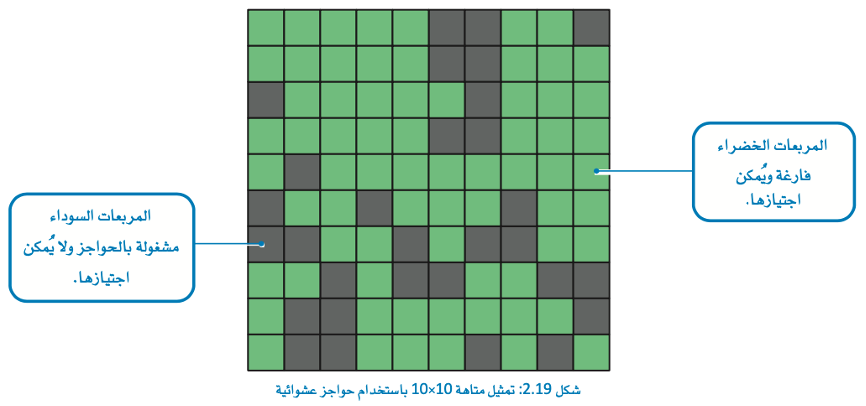
تعرف المتاهة في صورة إطار شبكي 3*3.

يحدد موضع البداية بنجمة في أسفل يسار المتاهة.

الهدف هو الوصول إلى الخلية المستهدفة المحددة بالعلامة X ويمكن للاعب الانتقال إلى أي خلية فارغة مجاورة لموقعه الحالي.

تكون الخلية فارغة إذا لم تحتوي على عائق. على سبيل المثال، المتاهة الموضحة في الشكل أعلاه تحتوي على 3 خلايا تشغلها الحواجز (Blocks).

هذه الحواجز الملونة باللون الرمادي تشكل عائقًا يجب على اللاعب تجاوزه للوصول إلى الهدف X ويمكن للاعب الانتقال بشكل أفقي أو رأسي أو قطري إلي أي خلية فارغة مجاورة لموقعه الحالي كما يظهر في الشكل أدناه:

الهدف هو إيجاد المسافة الأقصر والأقل عددًا لمرات فحص الخلايا، وبالرغم من أن المتاهة صغيرة 3*3 قد تبدو بسيطة للاعب البشري إلا أنه يتوجب على الخوارزمية الذكية إيجاد حلول للتعامل مع المتاهات الكبيرة والمعقدة للغاية مثل متاهة 10.000*10.000 التي تحتوي على ملايين الحواجز الموزعة في أشكال معقدة ومتنوعة.

يمكن استخدام المقطع البرمجي التالي بلغة بايثون لإنشاء مجموعة بيانات تصور المثال الموضح بالشكل أعلاه:

 في هذا التمثيل الرقمي للمتاهة تمثل الخلايا الفارغة بالأصفار (Zero) والمشغولة بالآحاد (One) يمكن تحديث المقطع البرمجي نفسه بسهولة لإنشاء متاهات كبيرة ومعقدة للغاية مثل:

تستخدم الدالة لتمثيل المتاهة:

يمكن استخدام الدالة التالية لاستدعاء قائمة تحتوي على كل الخلايا الفارغة والمجاورة لخلية محددة في أي متاهة:

يفترض هذا التطبيق أن كل عملية انتقال من خلية إلى أخرى مجاورة سواء أفقيًا أو رأسيًا أو قطريًا يتم بتكلفة مقدارها وحدة واحدة فقط. سيتم إعادة النظر في هذه الفرضية في وقت لاحق من هذا الدرس بعرض حالات أكثر تعقيدًا مع شروط انتقال متغيرة.

تستخدم كل خوارزميات البحث دالة get_accessible_neighbors() في محاولة حل المتاهة، في الأمثلة التالية تستخدم خلية 3*3 المصممة بالأعلى للتحقق من أن الدالة تستدعي الخلية الصحيحة والفارغة والمجاورة للخلية المحددة.

بعد أن تعلمت كيفية إنشاء المتاهات، وكذلك استدعاء الخلايا المجاورة لأي خليه في المتاهة، فإن الخطوة التالية هي تطبيق خوارزميات البحث التي يمكنها حل المتاهة من خلال إيجاد المسار الأقصر من خلية البداية إلى خلية الهدف المحددة.

بإمكانك مراجعة محتوى موضوع “خوارزميات البحث المستنيرة” من بدايته وحتى نهاية هذا القسم، من خلال الرابط التالي:

استخدام خوارزمية البحث بأولوية الاتساع في حل ألغاز المتاهة (Using BFS to Solve Maze Puzzles)

تستخدم دالة bfs_maze_solver() المشار إليها في هذا الجزء خوارزمية البحث بأولوية الاتساع (BFS) لحل ألغاز المتاهة باستخدام خلية البداية وخلية الهدف.

يستخدم هذا النموذج دالة get_accsible_neighbors() المحددة بالأعلى لاستدعاء الخلايا المجاورة التي يمكن فحصها عند أي نقطة أثناء البحث وبمجرد عثور خوارزمية البحث بأولوية الاتساع (BFS) على الخلية الهدف، ستستخدم دالة reconstruct_shortest_path() الموضحة بالشريحة التالية لإعادة بناء المسار الأقصر واستدعائه، وذلك بتتبع المسار بصورة عكسية من خلية الهدف إلى خلية البداية.

ستُستخدم دالة reconstruct_shortest_path() أيضًا لإعادة بناء الحل لخوارزمية البحث بأولوية الأفضل (A*search) المشار إليها سلفًا في هذا الدرس، وبالنظر إلى تعريف الدالتين get_accessible_neighbors() و reconstruct_shortest_path() المساعدتين، يمكن تنفيذ دالة bfs_maze_solver() على النحو التالي:

تتبع الدالة منهجية البحث بأولوية الاتساع (BFS) للبحث في كل الخيارات في العمق الحالي قبل الانتقال إلى مستوى العمق التالي وتستخدم هذه المنهجية مجموعة واحدة تسمى visited وقائمة تسمى to_expand.

تتضمن المجموعة الأولى كل الخلايا التي فحصت مرة واحدة على الأقل من قبل الخوارزمية بينما تتضمن المجموعة الثانية كل الخلايا التي لم توسع بعد، مما يعني أن الخلايا المجاورة لم تُفحص بعد.

تستخدم الخوارزمية كذلك قاموسين parent و shortest_distance يحفظ الأول منهما طول المسار الأقصر من خلية البداية إلى كل خلية أخرى، بينما يحفظ الثاني عقدة الخلية الأصل في المسار الأقصر.

بمجرد الوصول إلى الخلية الهدف وانتهاء البحث سيُخزن shortest_distance[target_cell] طول الحل والذي يمثل طول المسار الأقصر من البداية إلى الهدف.

يستخدم المقطع البرمجي التالي دالة maze_solver() لحل المتاهة الصغيرة 3*3 الموضحة بالأعلى:

تنجح خوارزمية البحث بأولوية الاتساع (BFS) في إيجاد المسار الأقصر بعد فحص 10 خلايا، يمكن تصوير عملية البحث المطبقة بخوارزمية البحث بأولوية الاتساع (BFS) بسهولة عند تصوير المتاهة بالتمثيل المستند إلى مخطط.

المثال التالي يعرض متاهة 3*3 وتمثليها بالمخطط:

يتضمن تمثيل المخطط عقدة واحدة لكل خلية غير مشغولة. توضح القيمة على العقد إحداثيات خلية المصفوفة المقابلة. ستظهر حافة غير موجهة من عقدة إلى أخرى في حال كانت الخلايا المقابلة يمكن الوصول إليها من خلال الانتقال من واحدة إلى أخرى.

إحدى الملاحظات المهمة حول خوارزمية البحث بأولوية الاتساع (BFS) هي أنه في حالة المخططات غير الموزونة (Unweighted Graph) يكون المسار الأول الذي تحدده الخوارزمية بين خلية البداية وأي خلية أخرى هو المسار الذي يتضمن أقل عدد من الخلايا التي تم فحصها.

وهذا يعني أنه إذا كانت كل الحواف في المخطط لها نفس الوزن، أي أنه كان لكل الانتقالات من خلية إلى أخرى التكلفة نفسها، فإن المسار الأول الذي تحدده الخوارزمية إلى عقدة محددة يكون هو المسار الأقصر إلى تلك العقدة. ولهذا السبب، تتوقف دالة bfs_maze_solver() عن البحث وتعرض نتيجة المرة الأولى التي فحصت فيها العقدة المستهدفة.

ومع ذلك لا يمكن تطبيق هذه المنهجية على المخططات الموزونة (Weighted Graphs)  المثال التالي يوضح إصدارًا موزونًا  (Weighted Version)لتمثيل مخطط المتاهة 3*3:

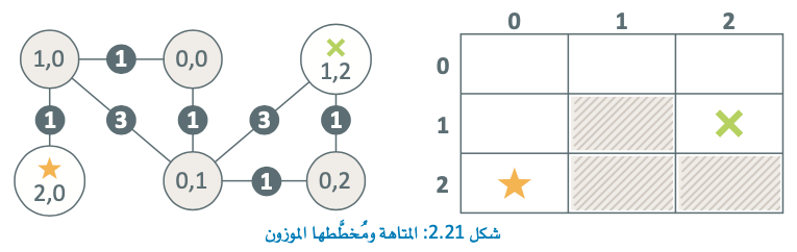
في هذا المثال، يكون وزن كل الحواف المقابلة للحركات الرأسية أو الأفقية (جنوبًا، شمالاً، غربًا، شرقًا) يساوي 1.

ومع ذلك يكون وزن كل الحواف المقابلة للحركات القطرية (جنوبية غربية، جنوبية شرقية، شمالية غربية، شمالية شرقية) يساوي 3 في هذه الحالة الموزونة سيكون المسار الأقصر هو ](0،2)، (0، 1)، (0،0)، (1، 0)، (2، 0)، (2، 1)[ بمسافة إجمالية 1+1+1+1+1=5.

يمكن ترميز هذه الحالة الأكثر تعقيدًا باستخدام الإصدار الموزون من الدالة get_accessible_neighbors()الموضحة بالأسفل:

تسمح الدالة للمستخدم بتعيين وزن مخصص للحركات الأفقية والحركات الرأسية وكذلك وزن مخصص مختلف للحركات القطرية. إذا استخدم الإصدار الموزون (Weighted Version) المشار إليه بواسطة أداة الحل في البحث بأولوية الاتساع (BFS Solver) فإن النتائج ستكون كما يلي:

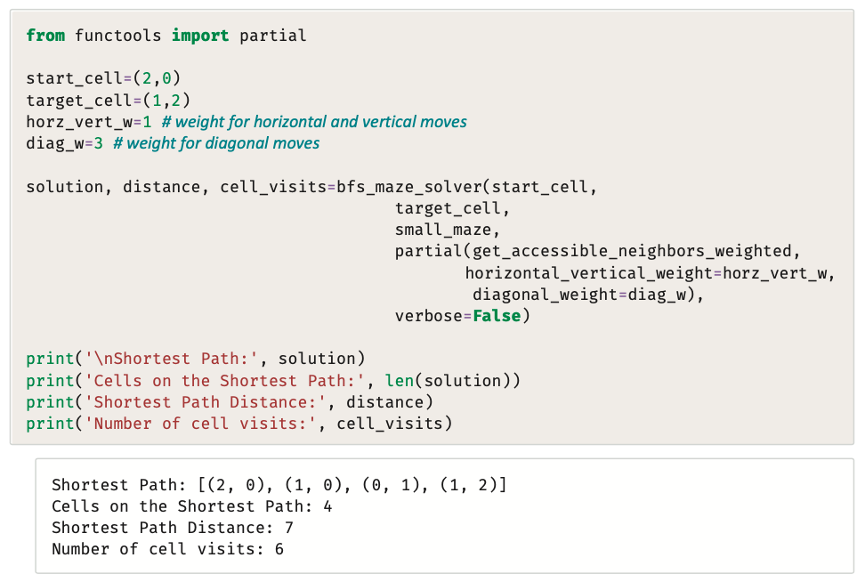
وكما هو متوقع، أخطأت أداة الحل في البحث بأولوية الاتساع (BFS solver) في عرض المسار نفسه بالضبط، على الرغم من أن التكلفة تساوي 7 ومن الواضح أنه ليس المسار الأقصر، ويرجع ذلك إلى الطبيعة غير المستنيرة لخوارزمية البحث بأولوية الاتساع (BFS)، حيث لا تأخذ الخوارزمية الأوزان بعين الاعتبار عند تحديد الخلية المقرر توسيعها في الخطوة التالية، لأنها تتطبق ببساطة منهجية البحث بالعرض نفسها والتي تؤدي إلى المسار نفسه الذي وجدته الخوارزمية في الإصدار غير الموزون (Unweighted Version) من المتاهة.

القسم التالي يصف طريقة معالجة نقطة الضعف هذه باستخدام خوارزمية البحث بأولوية الأفضل A*search وهي خوارزمية مستنيرة وأكثر ذكاءً تضبط سلوكها وفقًا للأوزان المحددة وبالتالي يمكنها حل المتاهات باستخدام الانتقالات الموزونة (Weighted Version) والانتقالات غير الموزونة (Unweighted Version).

بإمكانك مراجعة محتوى موضوع “خوارزميات البحث المستنيرة” بدايةً من عنوان “استخدام خوارزمية البحث بأولوية الاتساع في حل ألغاز المتاهة” وحتى نهاية هذا القسم، من خلال الرابط التالي:

استخدام خوارزمية البحث بأولوية الأفضل في حل ألغاز المتاهة (Using A* Search to Solve Maze Puzzles)

كما في خوارزمية البحث بأولوية الاتساع (BFS)، تُفحص خوارزمية البحث بأولوية الأفضل (A* search) خلية واحدةً كلّ مرّة، بفحص كلّ خليةٍ مجاورةٍ يمكن الوصول إليها. بينما تستخدم خوارزمية البحث بأولوية الاتساع (BFS) منهجية بحث عمياء بأولوية العرض لتحديد الخلية التالية التي ستفحصها، تُفحص خوارزمية البحث بأولوية الأفضل (A* search) الخلية التي يكون بينها وبين الخلية المستهدفة أقصر مسافة محسوبة بواسطة الدالة الاستدلالية (Heuristic Function). يعتمد التعريف الدقيق للدالة الاستدلالية عل التطبيق. في حالة ألغاز المتاهة توفرالدالة الاستدلالية تقديرًا دقيقًا لمدى قرب الخلية المُرشحة إلى الخلية المستهدفة. يضمن الاستدلال المطبق عدم المبالغة في تقدير (Overestimate) المسافة الفعلية إلى الخلية المستهدفة، مثل: عرض مسافة تقديرية أكبر من المسافة الحقيقية إلى الهدف، وبالتالي ستحدد الخوارزمية أقصر مسار لكل من المخططين الموزون (Weighted) وغير الموزون (Unweighted).

إذا كان الاستدلال يُبالغ في بعض الأحيان في تقدير المسافة، ستُقدم خوارزمية البحث بأولوية الأفضل (A* search) حلاً. ولكن قد لا يكون الأفضل، الاستدلال المحتمل الأبسط الذي لن يؤدي إلى المبالغة في تقدير المسافة هو دالة بسيطة تُعطي دوماً مسافة تقديرية قدرها وحدةً واحدة.

على الرغم من أن هذا الاستدلال شديد التفاؤل، إلا أنه لن يقدم أبدًا تقديرًا أعلى من المسافة الحقيقية وبالتالي سيؤدي إلى أفضل حل ممكن.

سيتم تقديم استدلال متطور يمكنه العثور على أفضل حل بشكل سريع في هذا القسم لاحقًا.

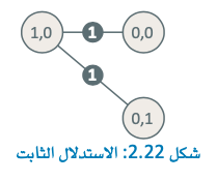
تستخدم الدالة التالية دالة استدلالية معطاة للعثور على الخلية التي يجب توسيعها بعد ذلك:

يستخدم التطبيق المشار إليه بالأعلى حلقة تكرار For لفحص الخلايا المرشحة في المجموعة وتحديد الأفضل.

ولتطبيق أكثر كفاءة قد يستخدم طابور الأولوية (Priority Queue) في تحديد المرشح الأفضل دون الحاجة إلى فحص كل المرشحين بصورة متكررة.

تستخدم دالة get_best_candidate() كدالة مساعدة بواسطة دالة aster_maze_solver() الموضحة فيما يلي. وبالإضافة إلى الدالة الاستدلالية يستخدم هذا التطبيق كذلك الدالتين المساعدتين get_accessible_neighbors() وreconstruct_shortest_path() المشار إليها في القسم السابق:

وكما في الحال دالة bfs_maze_solver()، تستخدم الدالة الموضحة بالأعلى كذلك القاموسين shortest_distance وparent لحفظ طول المسار الأقصر من خلية البداية وحفظ عقدة أصل الخلية في هذا المسار الأقصر.

ورغم ذلك، تتبع الدالة astar_maze_solve() منهجية مختلفة لفحص الخلايا وتوسيعها فهي تستخدم expansion_candidates لتتبع كل الخلايا التي يمكن توسيعها بعد ذلك، في كل تكرار، تستخدم دالة get_best_candidate() لتحديد أي من الخلايا المرشحة ستُوسعها بعد ذلك.

بعد اختيار الخلية المرشحة best_cell تستخدم حلقة التكرار for لفحص كل الخلايا المجاورة لها. إذا كانت الخلية المجاورة تُفحص للمرة الأولى فستصبح best_cell عقدة الأصل للخلية المجاورة.

يحدث الأمر نفسه إذا تم فحص الدالة المجاورة من قبل، ولكن فقط إذا كان المسار إلى هذه الخلية المجاورة من خلال best_cell أقصر من المسار السابق. إذا عثرت الدالة بالفعل على مسار أفضل فسيتعين على الحلية المجاورة العودة إلى مجموعة expansion_candidates لإعادة تقييم المسار الأقصر إلى الخلايا المجاورة لها.

يستخدم المقطع البرمجي التالي astzr_maze_solver() لحل الحالة غير الموزونة (Unweighted case) للغز المتاهة 3*3:

ستبحث أداة الحل في البحث بأولوية الأفضل (A*search algorithm) عن المسار المحتمل الأقصر والأفضل بعد فحص 12 خلية. وهذا أكثر قليلاً من أداة الحل في البحث بأولوية الاتساع (BFS Solver) التي وجدت الحل بعد فحص 10 خلايا فقط.

هذا يعود إلى بساطة الاستدلال الثابت المستخدم لإرشاد astar_maze_solver() وكما سيتضح لاحقًا في هذا القسم، يمكن استخدام دالة استدلال أخرى لتمكين الخوارزمية من إيجاد حل بشكل أسرع.

الخطو التالية هي تقييم ما إذا كانت خوارزمية البحث بأولوية الأفضل a*search قادرة على حل المتاهة الموزونة التي فشلت خوارزمية البحث بأولوية الاتساع (BFS) في العثور على أقصر مسار لها أم لا:

توضح النتائج قدرة astar_maze_solver() على حل الحالة الموزونة بالعثور على المسار الأقصر المحتمل ](2، 0)، (0،1)، (0،0)، (2،0)، (1،0)،(2،1)[ بتكلفة إجمالية قدرها 5. وهذا يوضح مزايا استخدام خوارزمية بحث مستنيرة فهي تمكنك من إيجاد الحل الأمثل باستخدام أبسط طريقة ممكنة.

بإمكانك مراجعة محتوى موضوع “خوارزميات البحث المستنيرة” بدايةً من عنوان “استخدام خوارزمية البحث بأولوية الأفضل في حل ألغاز المتاهة” وحتى نهاية القسم، من خلال الرابط التالي:

المقارنة بين الخوارزميات (Algorithm Comparison)

الخطوة التالية هي المقارنة بين خوارزمية البحث بأولوية الاتساع (BFS) وخوارزمية البحث بأولوية الأفضل (A*Search) في متاهة أكبر حجمًا ولأكبر تعقيدًا. يُستخدم المقطع البرمجي التالي بلغة البايثون لإنشاء تمثيل رقمي لهذه المتاهة.

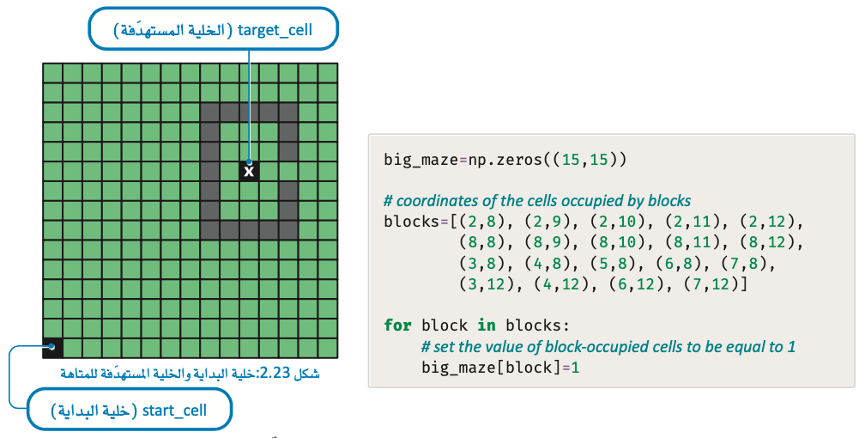
هذه المتاهة 15*15 تحتوي على قسم من الحواجز على شكل حرف C  ينبغي على اللاعب تجاوزها للوصول إلى الهدف المحدد بالعلامة X. ثم تستخدم أداة الحل في البحث بأولوية الاتساع (BFS Solver) وأداة البحث بأولوية الأفضل (A*Search) لحل الإصدارات الموزونة وغير الموزونة من هذه المتاهة كبيرة الحجم:

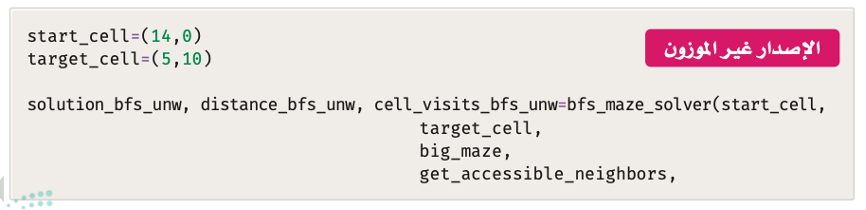
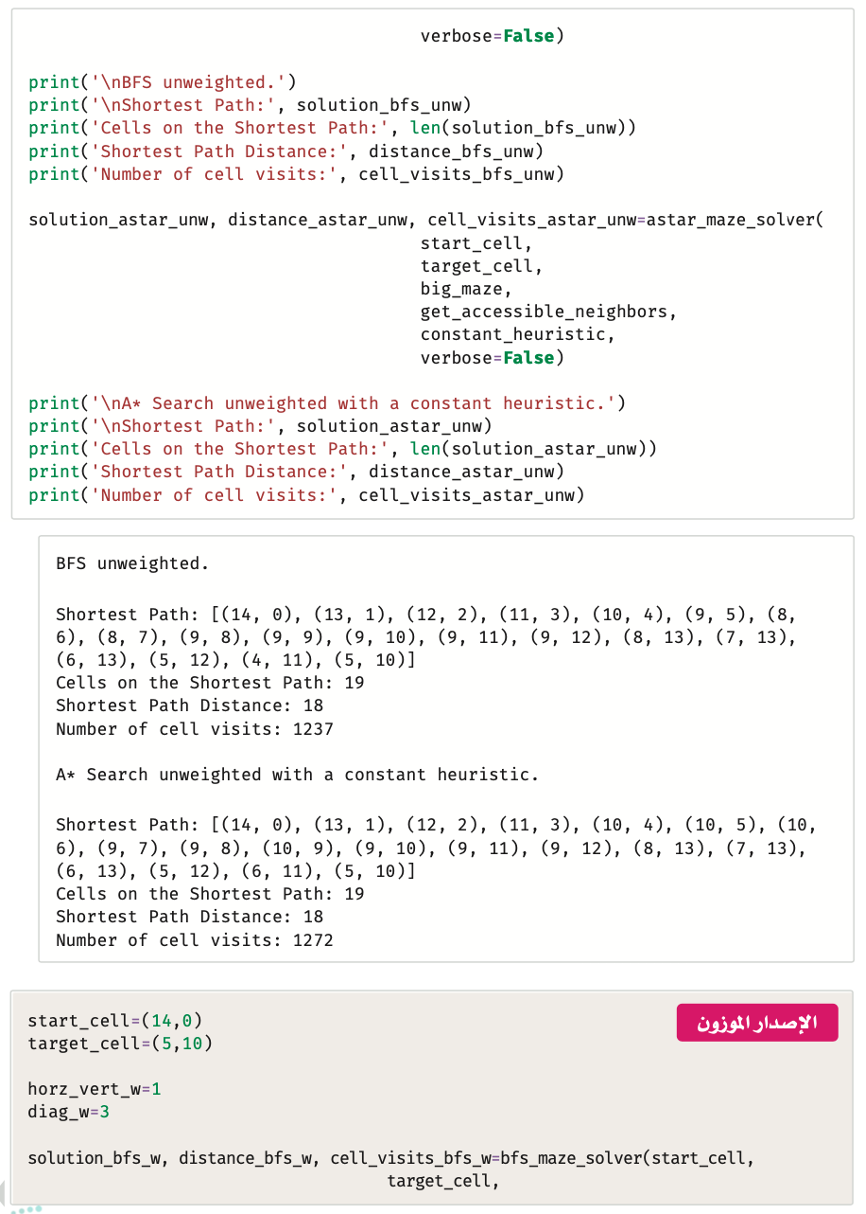
تتوافق النتائج مع تلك التي حصلت عليها في المتاهة وهي كالتالي:

• نجحت خوارزميتا البحث بأولوية الاتساع (BFS) والبحث بأولوية الأفضل (A*search) في العثور على المسار الأقصر للإصدار غير الموزون.
• وجدت خوارزمية البحث بأولوية الاتساع (BFS) الحل بعد فحص عدد أقل من الخلايا وهو 1237 مقابل 1272 في خوارزمية البحث بأولوية الأفضل (A*Search).
• فشلت خوارزمية البحث بأولوية الاتساع (BFS) في العثور على المسار الأقصر للإصدار الموزون حيث عثرت على مسار بطول 30 وحدة.
• عثرت خوارزمية البحث بأولوية الأفضل (A*Search) على المسار الأقصر للإصدار الموزون حيث عثرت على مسار بطول 25 وحدة.

يستخدم المقطع التالي لتمثيل المسار الأقصر الذي وجدته الخوارزميتان، خوارزمية البحث بأولوية الاتساع (BFS)وخوارزمية البحث بأولوية الأفضل (A*Search) للإصدار الموزون كالتالي:

يؤكد التمثيلان أن الطبيعة المستنيرة لخوارزمية البحث بأولوية الأفضل (A*Search) تسمح لها بتجنب الحركة القُطرية، لأن تكلفتها أعلى من الحركتين الأفقية والرأسية.

ومن ناحية أخرى، تتجاهل خوارزمية البحث بأولوية الأفضل (A*search)  غير المستنيرة تكلفة كل حركة وتعطي حلاً أعلى تكلفة.

فيما يلي مقارنة عامة بين الخوارزميات المستنيرة وغير المستنيرة كما هو موضح في الجدول أدناه:

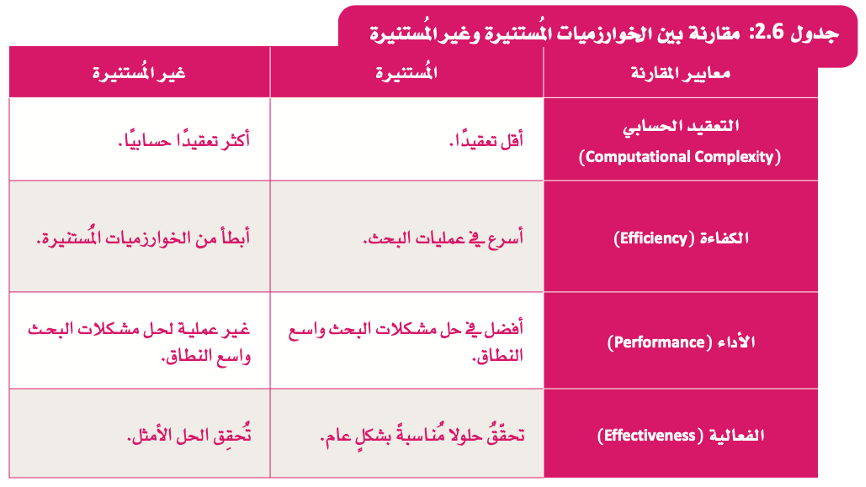
ومع ذلك تظهر النتائج أن خوارزمية البحث بأولوية الاتساع (BFS) يمكنها العثور على الحل الأمثل بشكل سريع بفحص عدد أقل من الخلايا في الحالة غير الموزونة، يمكن معالجة ذلك بتوفير استدلال أكثر ذكاءً لخوارزمية البحث بأولوية الأفضل (A*Search).

الاستدلال الشهير في التطبيقات المستندة إلى المسافة هو مسافة مانهاتن (Manhattan Distance) وهي مجموع الفروقات المطلقة بين إحداثيي نقطتين معطاتين.

يوضح الشكل أدناه، مثالاً على كيفية حساب مانهاتن:

مسافة مانهاتن:

يمكن تطبيق هذا بسهولة في صورة دالة البايثون كما يلي:

يُستخدم المقطع البرمجي التالي لاختبار إمكانية استخدام هذا الاستدلال الذكي لدعم astar_maze_solver() في البحث بشكل أسرع في كل من الحالات الموزونة وغير الموزونة:

تؤكد النتائج أن مسافة مانهاتن (Manhattan Distance) يمكن استخدامه لدعم خوارزمية البحث بأولوية الأفضل (A*Search) في العثور على المسارات الأقصر المحتملة بفحص أقل عدد من الخلايا في كل من الحالات الموزونة وغير الموزونة، علمًا بأن استخدام هذا الاستدلال الأكثر ذكاءً يفحص عددًا أقل من الخلايا من ذلك المستخدم في خوارزمية البحث بأولوية الاتساع (BFS).

يلخص الجدول التالي النتائج حول متغيرات الخوارزميات المختلفة في المتاهة الكبيرة:

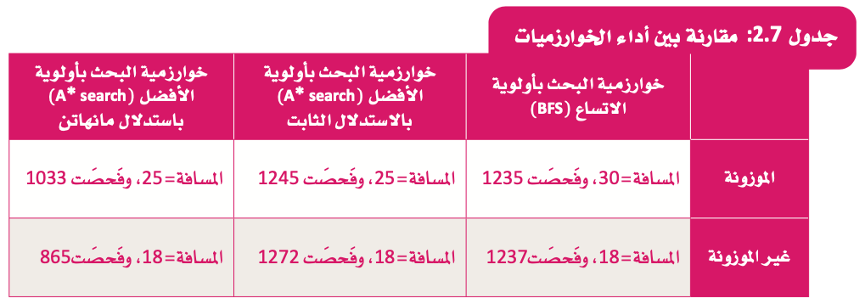
يوضح الجدول مزايا استخدام الطرائق الأكثر ذكاءً لحل المشكلات المستندة إلى البحث مثل تلك الموضحة بهذا الدرس:

• التحول من خوارزمية البحث بأولوية الاتساع (BFS) غير المستنيرة إلى خوارزمية البحث بأولوية الأفضل (A*Search) المستنيرة حقق أفضل نتائج، كما أتاح إمكانية حل المشكلات الأكثر تعقيدًا.
• يمكن تحسين ذكاء خوارزميات البحث المستنيرة باستخدام دوال الاستدلال الأفضل التي تسمح لها بالعثور على الحل الأمثل بشكل أسرع.

بإمكانك مراجعة محتوى موضوع “خوارزميات البحث المستنيرة” بدايةً من عنوان “المقارنة بين الخوارزميات” وحتى نهاية الموضوع، من خلال الرابط التالي:

اختبر تحصيلك لمحتوى الموضوع من خلال الرابط التالي:

الواجب الإلكتروني

إلى هنا يكون قد انتهى موضوع “خوارزميات البحث المستنيرة”، لا تنسوا مراجعة أهداف التعلُّم أعلى المقال، وانتظرونا في الموضوع القادم!

روابط هامة

مقررات الفصل الدراسي الأول