مشكلة جدولة الموارد | الوحدة الخامسة | الدرس الثاني

مشكلة جدولة الموارد هو عنوان الدرس الثاني من الوحدة الخامسة التي تحمل اسم “خوارزميات التحسين واتخاذ القرار” من مقرر “الذكاء الاصطناعي” الفصل الدراسي الثاني.

سنتعرف في هذا الموضوع على مشكلات الجدولة (Scheduling Problems) في مجال التحسين، واستخدام البايثون والتحسين لحل مشكلة التباطؤ الموزون للآلة الواحدة (Single-Machine Weighted Tardiness – SMWT) ومشكلة جدولة الإنتاج حسب الطلب (Job Shop Scheduling – JSS) وذلك من خلال تطبيق خوارزمية حل القوة المُفرطة (Brute-Force Solver)، وخوارزمية الحل الاستدلالية الجشعة (Greedy Heuristic Solver)، وخوارزمية حل البحث المحلي (Local Search Solver)، بالإضافة إلى المقارنة بين خوارزميات الحل.

لذا قم بقراءة أهداف التعلُّم بعناية، ثم أعد قراءتها وتأكَّد من تحصيل محتواها بعد انتهائك من دراسة الموضوع.

أهداف التعلُّم

• معرفة مشكلات الجدولة.
• معرفة مشكلة التباطؤ الموزون للآلة الواحدة.
• معرفة مشكلة جدولة الإنتاج حسب الطلب.
• استخدام البايثون والتحسين لحل مشكلة التباطؤ الموزون للآلة الواحدة.
• تطبيق خوارزمية حل القوة المُفرطة.
• تطبيق خوارزمية الحل الاستدلالية الجشعة.
• تطبيق خوارزمية حل البحث المحلي.
• مقارنة خوارزمية الحل.

هيا لنبدأ!

مشكلات الجدولة (Scheduling Problems)

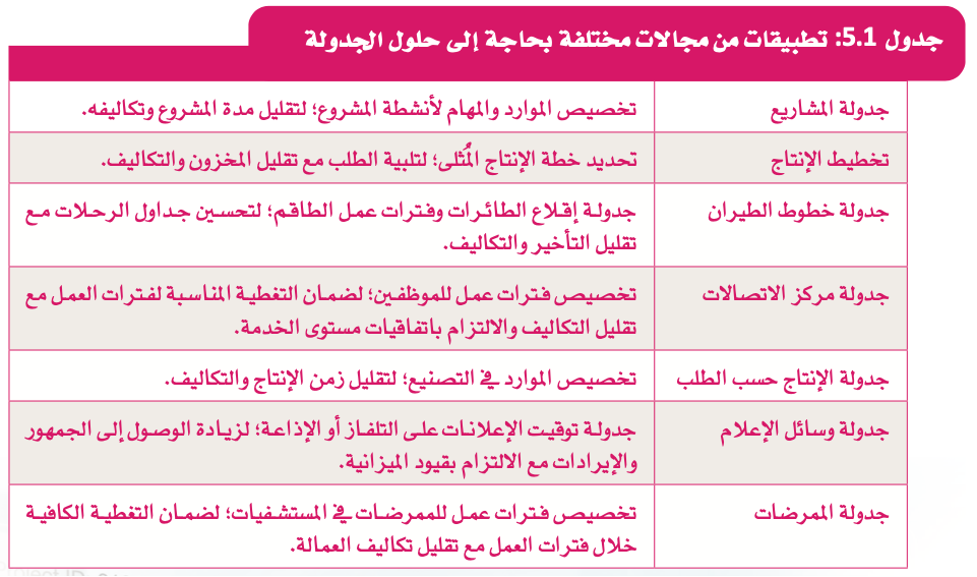
مشكلات الجدولة شائعة في مجال التحسين؛ لأنها تتطلَّب تخصيص موارد محدودة لمهام متعدِّدة بطريقة تُحسِّن بعض الدوال الموضوعية، وعادةً ما تكون لمشكلات الجدولة قيود إضافية، مثل: الحاجة إلى تنفيذ المهام بترتيب معيِّن أو إنجازها في الموعد النهائي المحدَّد، وهذه المشكلات جوهرية في العديد من المجالات المختلفة بما فيها التصنيع والنقل والرعاية الصحية وإدارة المشاريع.

لمعرفة المزيد عن مصطلح الجدولة، قم بالاطلاع على الرابط التالي:

جدولة (عمليات الإنتاج) – ويكيبيديا

ستتعمق في هذا الموضوع في خوارزميات التحسين عن طريق إدخال تقنيات إضافية لحل جدولة المشكلات.

في هذا الموضوع سيتم استخدام مشكلة التباطؤ الموزون للآلة الواحدة (Single-Machine Weighted Tardiness – SMWT) كمثال عملي لتوضيح كيف يمكِن لخوارزميات التحسين أن تحل مشكلات الجدولة.

مشكلة التباطؤ الموزون للآلة الواحدة (Single-Machine Weighted Tardiness Problem)

لتوضيح هذه المشكلة، سنفترض أن مصنعًا يرغب في جدولة مهام إنتاج عدة سلع على آلة واحدة، على النحو التالي:

• كل مهمَّة لها وقت معالجة محدَّد، وموعد محدَّد لابد أن تكتمل فيه.
• كل مهمَّة مرتبطة بوزن يمثل أهميتها.

إذا كان من المستحيل إنجاز كل المهام في الموعد النهائي، فسيكون عدم الالتزام بإنجاز المهام ذات الوزن الصغير في الموعد النهائي أقل تكلفة من عدم الالتزام بإنجاز المهام ذات الوزن الكبير في الموعد النهائي.

• الهدف

الهدف (Goal) من جدولة المهام بطريقة محدَّدة هو تقليل المجموع الموزون للتأخير (التباطؤ) لكل مهِمَّة، وهكذا فإن مجموع التباطؤ الموزون يكون بمثابة الدالة الموضوعية لخوارزميات التحسين المصمَّمة لحل هذه المشكلة.

• حساب التأخير

يُحسَبُ التأخير (Lateness) في أداء المُهِمَّة على أساس الفَرق بين زمن إنجازها والموعد المحدَّد لتسليمها، ثم يتم استخدام أوزان المهام كعوامل ضرب (Multipliers) لإكمال المجموع الموزون النهائي.

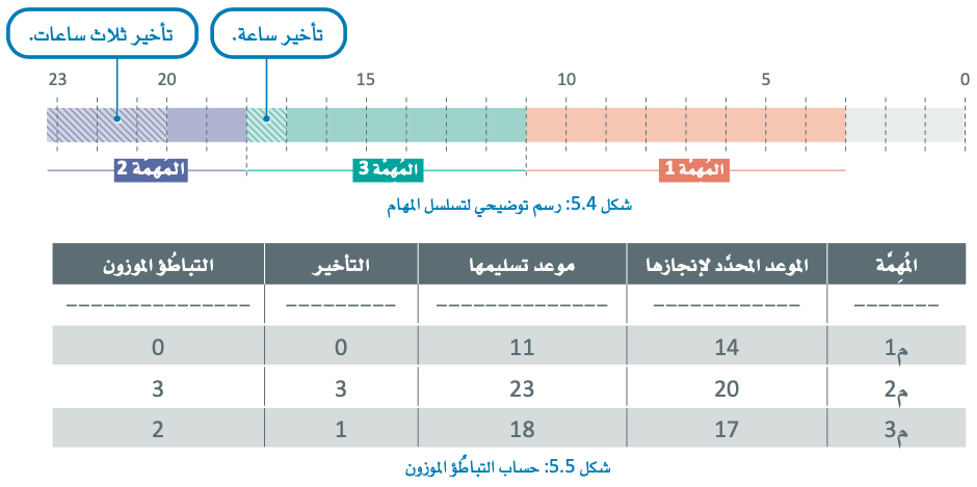
على سبيل المثال، افترض أن هناك جدولًا به 3 مهام، هي: م1 وم2 وم3، وأوزان هذه المهام هي: 2 و1 و2 على الترتيب.

وفقًا لهذا الجدول، ستقوم بإنجاز المُهِمَّة رقم 1 في الموعد المحدَّد، وسيتأخر إنجاز المُهِمَّة رقم 2 ثلاث ساعات عن موعد تسليمها، أما المُهِمَّة رقم 3 فسيتأخر إنجازها ساعة واحدة عن موعد تسليمها، ويعني ذلك أن مجموع التباطؤ الموزون يساوي 3*1+1*2=5.

توجد صعوبة في حل مشكلة التباطؤ الموزون للآلة الواحدة؛ لأن تعقُّدَها يتزايد تزايُدًا أسِّيًّا مع عدد المهام؛ مما يجعل إيجاد أفضل حل ممكن لأحجام المُدخَلات الكبيرة مكلفًا للغاية وعادةً ما يكون مستحيلًا.

لاحظ أن

يتم استخدام خوارزميات التحسين للحصول على حلول شبه مثالية لمشكلة محدَّدة في مدة زمنية معقولة.

مشكلة جدولة الإنتاج حسب الطلب (Job Shop Scheduling Problem)

مشكلة جدولة الإنتاج حسب الطلب (JSS) هي مشكلة اعتيادية أخرى في الجدولة حظيت بدراسات موسَّعة في مجال التحسين، وتتضمن جدولة مجموعة من المهام على عدة آلات، حيث يجب معالجة كل مهِمَّة بترتيب ووقت معيَّنان لكل آلة بالنسبة للمهام الأخرى.

• الهدف

تقليل زمن الإنجاز الكلي (فترة التصنيع) لجميع المهام.

• متغيِّرات المشكلة

المتغيِّرات الأخرى من هذه المشكلة تفرض عدة قيود إضافية، مثل:

• وجوب الالتزام بتاريخ إصدار كل مهِمَّة، حيث إن لكل مهِمَّة تاريخها الخاص ولا يمكِن البدء بها قبل ذلك التاريخ، بالإضافة إلى مراعاة الموعد النهائي.
• وجوب جدولة بعض المهام قبل المهام الأخرى، بسبب ضوابط الأسبقية بينها.
• وجوب إخضاع كل آلة للصيانة الدورية وفقًا لضوابط جدولة الصيانة، حيث لا يمكِن للآلات تأدية المهام أثناء الصيانة، كما لا يمكِن أن تتوقف المُهِمَّة بمجرد بدئها.

لابد أن تمر كل آلة بفترة توقُّف عن الإنتاج بعد إكمال الُمهِمَّة، وقد يكون طول هذه الفترة ثابتًا، وقد يتفاوت من آلة إلى أخرى، ومن الممكِن أن يعتمد على الوقت الذي استغرقته الآلة في إكمال المُهِمَّة السابقة.

ما ورد أعلاه ليس سوى مجموعة فرعية من القيود المعقَّدة والمتعدِّدة، ومن متغيِّرات المشكلة الموجودة في مشكلات الجدولة التي نواجها في واقع الحياة، حيث أن لكل متغيِّر خصائصه وتطبيقاته العملية الفريدة، وقد تكون خوارزميات التحسين المُختلفة أكثر ملاءمة لحل كل متغيِّر من متغيِّرات المشكلة.

استخدام البايثون والتحسين لحل مشكلة التباطؤ الموزون للآلة الواحدة (Using Python and Optimization to Solve the SMWT Problem)

يمكِن استخدام المقطع البرمجي التالي لإنشاء نُسَخ عشوائية لمشكلة التباطؤ الموزون للآلة الواحدة (SMWT):

يتم استخدام الدالة random.randint (x,y) لتوليد عدد صحيح عشوائي بين x وy، وهناك طريقة مختلفة لاستخدام هذه الدالة تتمثَّل في توفير قائمة [x,y] أو مجموعة (x,y)، وفي هذه الحالة لابد من كتابة الرمز * قبل القائمة، كما هو موضح في الدالة السابقة، على سبيل المثال:

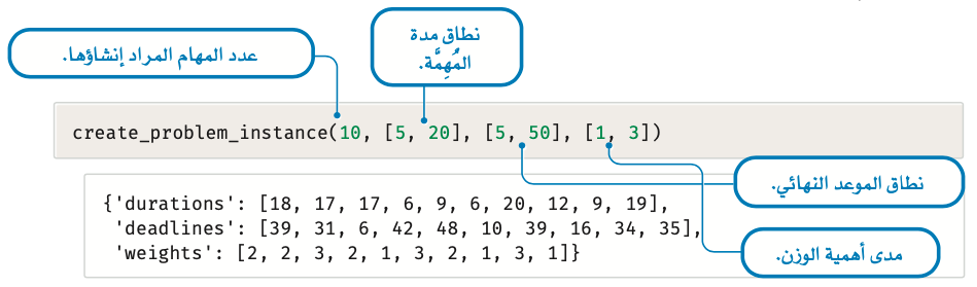
يَستخدِم المقطع البرمجي التالي دالة create_problem_instance() لتوليد نسخة لمشكلة يتوفر فيها ما يلي:

• تشتمل كل نسخة على 10 مهام.
• يمكِن لكل مهِمَّة أن تستمر ما بين 5 وحدات زمنية و20 وحدة زمنية، وسيتم افتراض أن الساعة هي الوحدة الزمنية المُستخدَمة فيما تبقَّى من هذا الموضوع.
• كل مهِمَّة لها موعد نهائي يتراوح ما بين 5 ساعات و50 ساعة، وتبدأ ساعة الموعد النهائي من لحظة بدء المُهِمَّة الأولى في استخدام الآلة، على سبيل المثال: إذا كان الموعد النهائي لمُهِمَّة ما يساوي 10 ساعات، فهذا يعني أنه لابد من إكمال المُهِمَّة في غضون 10 ساعات من بداية المُهِمَّة الأولى في الجدول.
• وزن كل مهِمَّة هو عدد صحيح يتراوح بين 1 و3.

يمكِن استخدام الدالة التالية لتقييم جودة أي جدول أنتجه إحدى الخوارزميات لنسخة مشكلة محدَّدة، حيث تَقبل الدالة نسخة المشكلة وجدولًا لمهامها، ثم تمر على كل المهام بترتيب جدولتها نفسه حتى تَحسب أزمنة إنجازها ومجموع التباطؤ الموزون لكامل الجدول، ويُحسب هذا التباطؤ بحساب تباطؤ كل مهِمَّة – مع مراعاة الموعد النهائي لها – وضربه في وزن المُهِمَّة وإضافة الناتج إلى المجموع:

سيتم استخدام الدالة compute_schedule_tardiness() لتقييم الجداول، وستكون هذه الدالة بمثابة أداة مفيدة لكل الخوارزميات التي سيتم تقديمها في هذا الموضوع لحل مشكلة التباطؤ الموزون للآلة الواحدة (SMWT).

دالة التباديل (Itertools.Permutations() Function)

تستخدِم خوارزمية حل القوة المُفرطة الدالة itertools.permutations() لإنشاء كل الجداول المُمكِنة (تجميعات المهام)، ثم تَحسِب تباطؤ كل جدول ممكِن وتستخرج أفضل جدول (الجدول ذو التباطؤ الكُلي الأدنى).

تقبل الدالة itertools.permutations() عنصرًا واحدًا متكررًا (مثل: قائمة) وتقوم بإنشاء كل تبديل ممكِن لقيم المُدخَلات، ويوضِّح المثال البسيط التالي استخدام دالة permutation() ويُظهِر التبديلات لكل عناوين المهام المُعطاة:

بإمكانك مراجعة محتوى موضوع “مشكلة جدولة الموارد” حتى نهاية هذا القسم، من خلال الرابط التالي:

خوارزمية حل القوة المُفرطة (Brute_Force Solver)

تعلمت في الموضوع السابق طريقة استخدام خوارزمية حل القوة المُفرطة في مشكلة تكوين فريق، وعلى الرغم من أن خوارزمية الحل هذه أظهرت بطئًا شديدًا في المشكلات الأكبر حجمًا؛ إلا أن قدرتها على إيجاد الحل الأمثل (أفضل حل ممكن) لنُسخ المشكلة ذات الحجم الصغير كانت مفيدة في تقييم جودة الحلول المُنتَجة بواسطة خوارزميات التحسين الأسرع التي لا تضمن إيجاد الحل الأمثل.

وبالمثل، يمكِن استخدام خوارزمية حل القوة المُفرطة التالية لحل مشكلة التباطؤ الموزون للآلة الواحدة (SMWT).

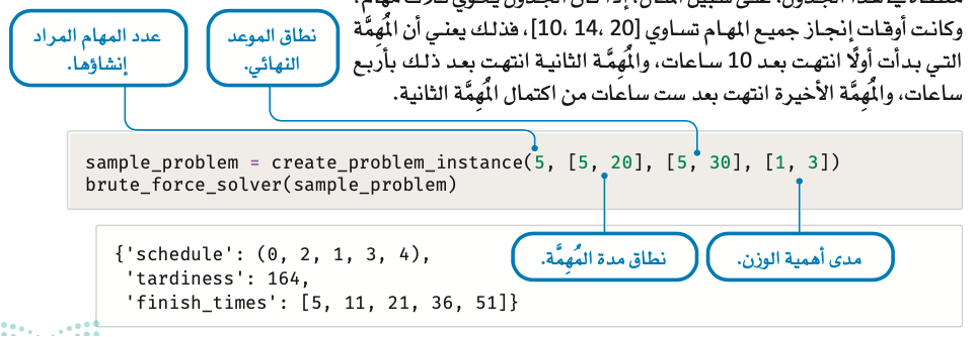
خوارزمية الحل تعطي الجدول الأفضل، وزمن التباطؤ، وزمن إنجاز كل مهِمَّة معطاة في هذا الجدول.

على سبيل المثال، إذا كان الجدول يحوي 3 مهام، وكانت أوقات إنجاز جميع المهام تساوي [10, 14, 20]، فذلك يعني أن المُهِمَّة التي بدأت أولًا انتهت بعد 10 ساعات، والمُهِمَّة الثانية انتهت بعد ذلك بأربع ساعات، والمُهِمَّة الأخيرة انتهت بعد 6 ساعات من اكتمال المُهِمَّة الثانية.

خوارزمية الحل الاستدلالية الجشعة (Greedy Heuristic Solver)

تستخدِم خوارزمية الحل الجشعة أسلوبًا استدلاليًا بسيطًا لفرز المهام واتخاذ قرار الترتيب الذي يجب جدولتها وفقًا له، ثم يتم ترتيب المهام لحساب زمن إكمال كل مهِمَّة ومجموع التباطؤ الموزون لكامل الجدول، وفي هذا المثال الخاص تُظهر خوارزمية الحل الجشعة نوع المُخرَجات نفسه الذي أظهرته خوارزمية حل القوة المُفرطة.

تَقبل خوارزمية الحل الجشعة معاملان هما: نسخة المشكلة المراد حلها، ودالة الاستدلال التي سيتم استخدامها (معيار فرز المهام)؛ مما يسمح للمُستخدِم بأن يطبِّق أي دالة استدلال يختارها كدالة البايثون. ثم يمرِّره إلى خوارزمية الحل الجشعة باعتباره معاملًا.

تُظهر الدالة التالية الموعد النهائي لمُهِمَّة محدَّدة في نسخة مشكلة معطاة:

تمرير دالة deadline_heuristic كمُعامِل إلى خوارزمية الحل الجشعة (greedy_solver) يعني أن الخوارزمية ستقوم بجدولة (تفرز) المهام وفق ترتيب تصاعدي حسب الموعد النهائي؛ مما يعني أن المهام التي لها أقرب موعد نهائي سيتم جدولتها أولًا.

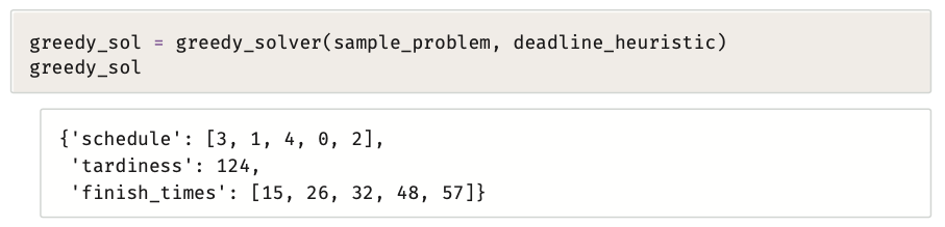
تطبِّق الدالة التالية استدلالًا بديلًا يأخذ في اعتباره أوزان المهام عند اتّخاذ قرار ترتيبها في الجدول:

بإمكانك مراجعة محتوى موضوع “مشكلة جدولة الموارد” بدايةً من عنوان “خوارزمية حل القوة المفرطة” حتى نهاية هذا القسم، من خلال الرابط التالي:

البحث المحلي (Local Search)

البحث المحلي (Local Search)

هو طريقة تحسين استدلالية تركِّز على اكتشاف حلول مجاورة لحل معيَّن بهدف تحسينه.

على الرغم من أن خوارزمية الحل الجشعة أسرع بكثير من خوارزمية القوة المُفرطة؛ إلا أنها تميل إلى إنتاج حلول ذات جودة أقل بزمن تباطؤ أعلى، ويعدُّ البحث المحلي طريقة لتحسين حل تم حسابه بواسطة الخوارزمية الجشعة أو بأي طريقة أخرى.

في البحث المحلي، يتم تعديل الحل الذي تك التوصل إليه في البداية بشكلٍ متكرِّر من خلال فحص الحلول المجاورة التي وجدِت عن طريق إجراء تعديلات بسيطة على الحل الحالي.

بالنسبة للعديد من مشكلات التحسين، فهناك طريقة شائعة لتعديل الحل تتمثل في تبديل العناصر بشكلٍ متكرِّر.

على سبيل المثال، في مشكلة تكوين الفريق التي تم توضيحها في الموضوع السابق، سيحاول أسلوب البحث المحلي إنشاء فريق أفضل، وذلك من خلال تبديل أعضاء الفريق بالعمَّال الذين لا يعدّون حاليًا جزءًا من الفريق.

أنشأت خوارزمية الحل الاستدلالية الجشعة (Greedy Heuristic Solver) حلًّا للمشكلة خطوة خطوة حتى حصلت في النهاية على حل كامل ونهائي، وعلى العكس من ذلك تبدأ طرائق البحث المحلية بحل كامل قد يكون ذا جودة متوسطة أو سيئة، وتعمل بطريقة تكرارية لتحسين جودته.

في كل خطوة يكون هناك تغيير بسيط على الحل الحالي، ويتم تقييم جودة الحل الناتج (يسمى الحل المجاور)، وإذا كان يتمتع بجودة أفضل، فإنه يستبدل الحل الحالي ويستمر في البحث، وإذا لم يكن كذلك، يتم تجاهل الحل المجاور، وتتكرَّر العملية لتوليد حل مجاور آخر، ثم ينتهي البحث عندما يتعذر العثور على حل مجاور آخر يتمتع بجودة أفضل من الحل الحالي، ويتم تحديد أفضل حل تم العثور عليه.

دالة خوارزمية حل البحث المحلي (Local_search_solver() Function)

تطبق الدالة التالية local_search_solver() خوارزمية حل البحث المحلي القائم على المُبادلة لمشكلة التباطؤ الموزون للآلة الواحدة (SMWT)، حيث تقبل هذه الدالة 4 معامِلات، وهي:

1. نسخة المشكلة.
2. خوارزمية استدلالية جشعة تستخدِمها دالة greedy_solver() لحساب حل أوّلي.
3. دالة swap_selector المُستخدَمة لانتقاء مهمَّتين ستتبادلان موقعيهما في الجدول. على سبيل المثال، إذا كان الحل الحالي للمشكلة المكوَّنة من 4 مهام هو [0, 2, 3, 1]، وقرَّرت دالة swap_selector أن يحدث مبادلة بين المُهِمَّة الأولى والمُهِمَّة الأخيرة، سيكون الحل المرشَّح هو [1, 2, 3, 0].
4. max_iterarions عدد صحيح يحدِّد عدد المبادلات التي يجب تجربتها قبل أن تتوصل الخوارزمية للحل الأفضل في حينه.

في كل تكرار، تنتقي الخوارزمية مهِمَّتين للتبديل بينهما، ثم تقوم بإنشاء جدولًا جديدًا تتم فيه هذه المبادلة، وكل شيء في الجدول الجديد بخلاف ذلك سيكون مطابقًا للجدول الأصلي.

إذا كان للجدول الجديد تباطؤ موزون أقل من الجدول الأفضل الذي تم إيجاده حتى الآن، فإن الجدول الجديد يصبح هو الأفضل بدلًا منه.

خوارزمية الحل هذه لها نفس مخرَجات خوارزمية الحل الجشعة وخوارزمية حل القوة المُفرطة.

لاحظ أن

سلوك خوارزميات التحسين القائمة على البحث المحلي بتأثر بشكل كبير بالاستراتيجية المُستخدَمة بطريقة تكرارية لتعديل الحل.

تطبِّق الدالة التالية مبادلة عشوائية بانتقاء مهِمَّتين عشوائيتين في الجدول المُعطى الذي يستوجب تبديل مكانيهما:

تستخدِم الدالة التالية استراتيجية مختلفة وذلك باختيارها الدائم لمهِمَّتين عشوائيتين متجاورتين في الجدول لتبادلهما.

على سبيل المثال، إذا كان الجدول الحالي لنسخة مشكلة مكوَّنة من 4 مهام هو [0, 3, 1, 2]، فإن المبادلات المُرشَّحة فقط 3<>0 و1<>3 و2<>1.

يستخدِم المقطع البرمجي التالي استراتيجيتي المبادلة مع خوارزمية حل البحث المحلي لحل المشكلة التي تم إنشاؤها في بداية هذا الموضوع:

تقوم النتائج بإظهار أفضل جدول [3, 4, 2, 1, 0] لهذا المثال، وإجمالي التباطؤ 83، وأزمنة إكمال المهام (ستنتهي المُهِمَّة 3 في الوحدة 15 من الزمن، وتنتهي المُهِمَّة 4 في الوحدة 21 منه، وهكذا).

مقارنة خوارزمية الحل (Comparing Solvers)

يستخدِم المقطع البرمجي التالي الدالة create_problem_instance لتوليد مجموعتي بيانات:

• مجموعة بيانات من 100 نسخة لمشكلة التباطؤ الموزون للآلة الواحدة، وفي كلٍ منها 7 مهام.
• مجموعة بيانات من 100 نسخة لمشكلة التباطؤ الموزون للآلة الواحدة، وفي كلٍ منها 30 مهِمَّة.

سيتم استخدام مجموعة البيانات الأولى لمقارنة أداء جميع خوارزميات الحل الموضَّحة في هذا الموضوع:

1. خوارزمية حل القوة المُفرطة.
2. خوارزمية الحل الجشعة المُتضمنة على استدلال خاص بالموعد النهائي.
3. خوارزمية الحل الجشعة المُتضمنة على استدلال خاص بالموعد النهائي الموزون.
4. خوارزمية حل البحث المحلَي المُتضمنة على مبادلات عشوائية وخوارزمية الحل الجشعة ذات استدلال خاص بالموعد النهائي لإيجاد الحل الأوَّلي.
5. خوارزمية حل البحث المحلَي المُتضمنة على مبادلات عشوائية وخوارزمية الحل الجشعة ذات استدلال خاص بالموعد النهائي الموزون.
6. خوارزمية حل البحث المحلّي المُتضمنة على مبادلات متجاورة وخوارزمية الحل الجشعة ذات استدلال خاص بالموعد النهائي.
7. خوارزمية حل البحث المحلّي المُتضمنة على مبادلات متجاورة وخوارزمية الحل الجشعة ذات استدلال خاص بالموعد النهائي الموزون.

سيتم استخدام مجموعة البيانات الثانية لمقارنة جميع خوارزميات الحل باستثناء خوارزمية حل القوة المُفرطة البطيئة جدًا بالنسبة للمشكلات المشتملة على 30 مهِمَّة.

دالة المقارنة (Compare() Function)

تستخدِم الدالة التالية compare() كل خوارزميات الحل؛ لحل كل المشكلات في مجموعة بيانات معيَّنة، ثم تُظهر متوسط التباطؤ الذي تحققه كل خوارزمية حل على كل المشكلات في مجموعة البيانات، وتقبل الدالة كذلك المُعامِل المنطقي use_brute لتحديد إمكانية استخدام خوارزمية الحل بالقوة المُفرطة أم لا:

يمكِن الآن استخدام دالة compare() مع مجموعتي البيانات problems_7 وproblems_30 كلتيهما:

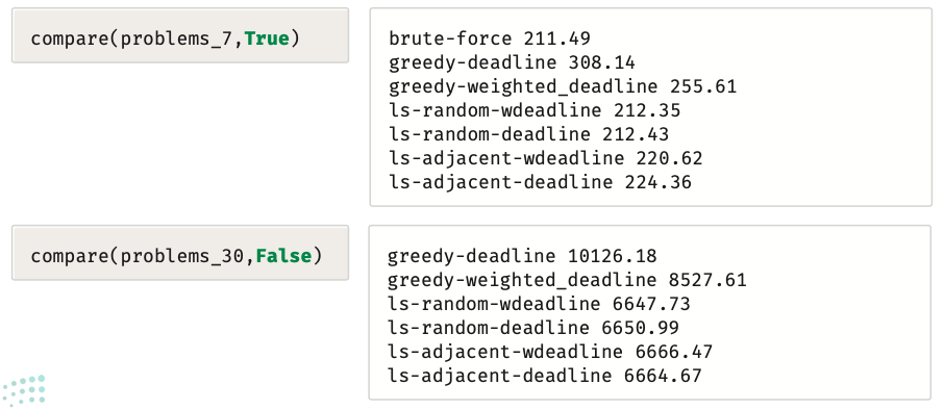
بإمكانك مراجعة محتوى موضوع “مشكلة جدولة الموارد” بدايةً من عنوان “البحث المحلي” وحتى نهاية الموضوع، من خلال الرابط التالي:

إلى هنا يكون قد انتهى موضوع “مشكلة جدولة الموارد“، لا تنسوا مراجعة نواتج التعلُّم أعلى المقال، وانتظرونا في الموضوع القادم!

روابط هامة

مقررات الفصل الدراسي الثاني