مشكلة تخصيص الموارد | الوحدة الخامسة | الدرس الأول

مشكلة تخصيص الموارد هو عنوان الدرس الأول من الوحدة الخامسة التي تحمل اسم “خوارزميات التحسين واتخاذ القرار” من مقرر “الذكاء الاصطناعي” الفصل الدراسي الثاني.
سنتعرف في هذا الموضوع على خوارزميات التحسين (Optimization Algorithms) في الذكاء الاصطناعي، واتخاذ القرار بخوارزمية القوة المُفرطة (Brute-Force Algorithm)، وغيرها من المواضيع الهامة.

مشكلة تخصيص الموارد
لذا قم بقراءة أهداف التعلُّم جيدًا، ثم أعد قراءتها وتأكَّد من تحصيل محتواها بعد انتهائك من دراسة الموضوع.
أهداف التعلُّم
- معرفة خوارزميات التحسين في الذكاء الاصطناعي.
- اتخاذ القرار باستخدام خوارزمية القوة المُفرطة.
- اتخاذ القرار باستخدام خوارزمية استدلالية جشعة.
- مقارنة الخوارزميات.
هيا لنبدأ!
خوارزميات التحسين في الذكاء الاصطناعي (Optimization Algorithms in AI)
يتم استخدام الذكاء الاصطناعي في مختلف الصناعات لاتّخاذ قرارات تتسم بالكفاءة والدقة، ويعتبر استخدام خوارزميات تعلُّم الآلة إحدى طرائق الذكاء الاصطناعي المُستخدَمة في اتّخاذ القرارات.
وكما تعلَّمت في الوحدة السابقة، فإن خوارزميات تعلُّم الآلة تقوم بتمكين الذكاء الاصطناعي من التعلُّم بواسطة البيانات، ومن ثمّ القيام بالتنبؤات أو تقديم التوصيات.
على سبيل المثال، في مجال الرعاية الصحية، من الممكن استخدام الذكاء الاصطناعي للتنبؤ بنتائج المرضى والتوصية بخُطط علاجية بناءً على البيانات التي تم جمعها من حالات مماثلة.
وفي مجال التمويل، من الممكن استخدام الذكاء الاصطناعي في اتّخاذ قرارات استثمارية بواسطة تحليل مجموعات كبيرة من البيانات المالية وتحديد الأنماط التي تبيِّن المخاطر أو الفرص المحتملة.

مشكلة تخصيص الموارد
وعلى الرغم من أن خوارزميات تعلُّم الآلة تحظى بشعبية متزايدة إلا أنها ليست النوع الوحيد من خوارزميات الذكاء الاصطناعي التي يمكن استخدامها في اتّخاذ القرارات، فهناك طريقة أخرى تتمثل في استخدام خوارزميات التحسين التي يتم استعمالها بوجه عام لإيجاد أفضل حل لمشكلة محدَّدة بناءً على قيود وأهداف معيَّنة.
يهدف التحسين إلى تحقيق التصميم الأفضل بالنسبة لمجموعة من المعايير أو القيود ذات الأولوية، وتشمل تعزيز عوامل معيَّنة، مثل: الإنتاجية، الموثوقية، طول العمر، والكفاءة، وفي الوقت نفسه تقليل عوامل أخرى، مثل: التكاليف، الفاقد، التوقُّف عن العمل، والأخطاء.
تعريفات هامة
القيود (Constraints)
هي بمثابة شروط تقيِّد الحل، مثل الحد الأقصى لوزن الطرد الذي يمكِن شحنه.
الدوال الموضوعية (Objective Functions)
هي معايير تحدِّد مدى اقتراب الحل المقدَّم من النتائج المطلوبة، مثل تقليل مسافة السفر لشاحنة توصيل.
لمعرفة المزيد عن خوارزميات التحسين في الذكاء الاصطناعي، قم بالاطلاع على الرابط التالي:
مشكلات التخصيص (Allocation Problems)
تعتبر مشكلات التخصيص من مشكلات التحسين الشائعة؛ ففيها يتم تخصيص مجموعة من الموارد، مثل: العمّال، أو الآلات، أو الأموال لمجموعة من المهام أو المشاريع بأعلى كفاءة ممكنة، وتنشأ هذه المشكلات في مجموعة واسعة من المجالات بما فيها التصنيع والخدمات اللوجستية وإدارة المشاريع والتمويل، ومن الممكن صياغتها بطرائق مختلفة بناءً على قيودها وأهدافها.
في هذا الموضوع ستتعرَّف على مشكلات التخصيص وخوارزميات التحسين المُستخدَمة لحلَّها.

مشكلة تخصيص الموارد
بعد ذلك، ستشاهد عددًا من الأمثلة، ولكل مثال منها قيود ودوال موضوعية خاصة به.

من الممكن نمذجة كل التطبيقات الواردة سابقًا في صورة مشكلات معقَّدة لها عدد كبير من الحلول المُمكنة.
على سبيل المثال، فكِّر في مشكلة تخصيص الموارد المعهودة التي تركِّز على تشكيل فريق، حيث تنشأ المشكلة عندما يكون لديك:
- مجموعة كبيرة من العمَّال يمتلكون مهارات مختلفة.
- مهمَّة تتطلَّب مجموعً فرعية محدَّدة من المهارات لأجل إكمالها.
ويتمثَّل الهدف في تكوين فريق بأقل عدد ممكن من العمَّال، مع الالتزام في الوقت نفسه بالقيد (Constraint) الذي ينصّ على توفُّر جميع المهارات المطلوبة في أعضاء الفريق؛ لأداء المُهِمَّة.

الطبيعة الخاصّة بأسلوب القوة المُفرطة تضمن دائمًا إيجاد الحل الأمثل، متى أمكن ذلك، ولكن فحص كل الفِرق المُمكنة يعتبر عملية مكلِّفة حاسوبيًّا، فمثلًا:
- إذا كان لديك 6 عمَّال، فسيكون عدد الفِرق المُمكِنة: 26 – 1 = 63.
- إذا كان لديك 10 عمَّال، فسيكون عدد الفِرق المُمكِنة: 210 – 1 = 1,023.
- إذا كان لديك 15 عمَّال، فسيكون عدد الفِرق المُمكِنة: 215 – 1 = 32,767.
- إذا كان لديك 20 عمَّال، فسيكون عدد الفِرق المُمكِنة: 220 – 1 = 1,048,575.
- إذا كان لديك 50 عمَّال، فسيكون عدد الفِرق المُمكِنة: 250 – 1 = 1,125,899,906,842,623.
لاحظ أن
حتى بالنسبة لعدد معتدل من 50 عاملًا، فإن عدد الفرق المحتملة يتضخم إلى أكثر من كوادريليون (Quadrillion = 1015)
من الواضح في مثل هذه المواقف أن حصر عدد الفِرق لكل الحلول المُمكِنة ليس خيارًا عمليًّا، ولذلك تم اقتراح طرائق تحسين أخرى لمعالجة المشكلات المعقَّدة عن طريق البحث في خيارات الحلول المُمكِنة بأسلوب أكثر كفاءة من أسلوب القوة المُفرطة، ومن الممكن بوجه عام تصنيف هذه الطرائق في 3 فئات:
- طرائق الاستدلال (Heuristic Methods)
- البرمجة القيدية (Constraint Programming)
- البرمجة الرياضية (Mathematical Programming)
بإمكانك مراجعة محتوى موضوع “مشكلة تخصيص الموارد” حتى نهاية هذا القسم من خلال الرابط التالي:
الحل الأمثل (Optimal Solution)
من الممكن أن تكون هناك العديد من الحلول المُثلى، كأن يكون لديك عدة فِرق تشمل 3 عمَّال وبإمكانها أن تستوفي كل المهارات المطلوبة، كما أنه من الممكن ألا يوجد حل لبعض المشكلات، على سبيل المثال: إذا كانت المُهِّمة تتطلَّب المهارة السابعة وهي لا تتوفَّر في أي عامل من العمَّال، فلن يكون هناك حل للمشكلة.
طرائق الاستدلال (Heuristic Methods)
تقوم طرائق الاستدلال (Heuristic Methods – HM) في العادة على التجربة، أو البديهية، أو الفطرة السليمة، وليس على التحليل الرياضي الدقيق، ومن الممكن استخدامها لإيجاد حلول جيدة بشكل سريع، ولكنها لا تضمن الوصول إلى الحل الأمثل (أفضل حل يمكن الحصول عليه)، ومن الأمثلة على الخوارزميات الاستدلالية؛ الخوارزميات الجشعة (Greedy Algorithms)، ومحاكاة التلدين (Simulated Annealing)، والخوارزميات الجينية (Genetic Algorithms)، وتحسين مستعمرة النمل (Ant Colony Optimizations).
يتم استخدام هذه الطرائق في العادة لحل المشكلات المعقَّدة التي تستغرق وقتًا حاسوبيًا طويلًا جدًّا، ولكن لا يمكنها إيجاد حلول دقيقة، وستتعلَّم في الدروس القادمة المزيد عن هذه الخوارزميات.
- الإيجابيات
تتميز الاستدلالات بالكفاءة الحاسوبية، وبإمكانها أن تتناول المشكلات المعقَّدة، كما بإمكانها أن تجد حلولًا ذات جودة عالية إذا استُخدِمت لها استدلالات معقولة.
- السلبيات
لا تضمن الوصول إلى الحل الأمثل، كما أن بعض الاستدلالات تتطلَّب ضبطًا كبيرًا حتى تؤدي إلى نتائج جيدة.
البرمجة القيدية (Constraint Programming)
البرمجة القيدية (Constraint Programming – CP) تحل مشكلات التحسين عن طريق نمذجة القيود وإيجاد حل يخضع لجميع القيود، وهذا الأسلوب مفيد بشكل خاص في المشكلات التي بها عدد كبير من القيود أو التي تتطلَّب تحسين عدة أهداف.
- الإيجابيات
من الممكن للبرمجة القيدية أن تتعامل مع قيود معقَّدة وأن تجد أفضل الحلول.
- السلبيات
من الممكن أن تكون هذه الطرائق مكلَّفة حاسوبيًّا في المشكلات الكبيرة.
البرمجة الرياضية (Mathematical Programming)
البرمجة الرياضية (Mathematical Programming – MP) هي مجموعة من التقنيات التي تَستخدِم نماذج رياضية؛ لحل مشكلات التحسين، وتشمل: البرمجة الخطية (Linear Programming)، والبرمجة الرباعية (Quadratic Programming)، والبرمجة غير الخطية (Nonlinear Programming)، وبرمجة الأعداد الصحيحة المختلطة (Mixed-Integer Programming)، ويتم استخدام هذه التقنيات على نطاق واسع في الكثير من المجالات؛ بما فيها علم الاقتصاد والهندسة وعمليات البحث.
تلعب أساليب البرمجة الرياضية دورًا مهمًا في التعلُّم العميق (Deep Learning)، وتمتلك نماذج التعلُّم العميق عددًا كبيرًا من المُعامِلات التي تحتاج أن تتعلَّم من البيانات، حيث يتم استخدام خوارزميات التحسين لتعديل معامِلات النموذج من أجل تقليل دالة التكلفة التي تقيس الفَرق بين مخرَجات النموذج المتنبّأ بها والمُخرَجات الصحيحة.
تم تطوير العديد من خوارزميات التحسين الخاصة بنماذج التعلُّم العميق، مثل: خوارزمية آدم (Adam)، خوارزمية الاشتقاق التكيُّفي (AdaGrad)، وخوارزمية نشر متوسط الجذر التربيعي (RMSprop).
- الإيجابيات
تتعامل البرمجة الرياضية مع مجموعة واسعة من مشكلات التحسين، وهي غالبًا تضمن الوصول إلى الحل الأمثل.
- السلبيات
تعتبر كلٍّ من التكلفة الحاسوبية للمشكلات الكبيرة وتعقيد إنشاء الصيغة الرياضية المناسبة مرتفعين بالنسبة لمشكلات العالم الواقعي المعقَّدة.
مثال عملي: تحسين مشكلة تشكيل الفريق (A Working Example: Optimization for the Team-Formation Problem)
سيوضِّح هذا الموضوع استخدام خوارزمية القوة المُفرطة (Brute-Force Algorithm)، والخوارزمية الاستدلالية الجشعة (Greedy Heuristic Algorithm) لحل مشكلة اتّخاذ القرار المُرتكزة على مشكلة تخصيص الموارد القائمة على الفريق والتي تم وصفها سابقًا، بعد ذلك ستتم مقارنة نتائج هاتين الخوارزميتين.
الخوارزمية الاستدلالية الجشعة (Greedy Heuristic Algorithm)
هي أسلوب استدلالي لحل المشكلات، وفيه تقوم الخوارزمية ببناء الحل خطوةً خطوة، وتختار الخيار الأمثل محليًّا في كل مرحلة؛ حتى تصل في النهاية إلى حل شامل ونهائي.
من الممكن استخدام الدالة التالية لإنشاء أمثلة عشوائية لمشكلة تشكيل الفرق، وتسمح هذه الدالة للمستخدِم أن يقوم بتحديد 4 معاملات هي: العدد الإجمالي للمهارات التي يجب أن تؤخذ بعين الاعتبار، والعدد الإجمالي للعمَّال المتوفِّرين، وعدد المهارات التي يجب أن تتوفَّر في أعضاء الفريق بشكل جماعي حتى ينجزوا المهمَّة، والعدد الأقصى للمهارات التي من الممكن أن يمتلكها كل عامل.
وبعد ذلك، تقوم الدالة بإنشاء وإظهار مجموعة عمَّال لديهم عدة مهارات مختلفة، وعدة مهارات مطلوبة، وتَستخدِم هذه الدالة المكتبة الشهيرة Random التي من الممكن استخدامها في إخراج عيِّنة أعداد عشوائية من مجموعة أعداد معيَّنة أو عناصر عشوائية من قائمة معيَّنة.

مشكلة تخصيص الموارد

ستقوم الآن باختبار الدالة الواردة سابقًا من خلال إنشاء نسخة من مشكلة معطياتها كالتالي: 10 مهارات إجمالية، 6 عمَّال، وتتطلَّب 5 مهارات كحدٍّ أقصى لكل عامل.

لاحظ أن
بسبب الطبيعة العشوائية للدالة، ستحصل على نسخة مختلفة من المشكلة في كل مرة تقوم فيها بتشغيل هذا المقطع البرمجي.

تتمثل الخطوة التالية في إنشاء خوارزمية حل (Solver)، وهي خوارزمية تحسين بإمكانها أن تحدِّد أقل عدد ممكن لفريق العمَّال الذي يمكن اعتماده لاستيفاء كل المهارات المطلوبة.
اتخاذ القرار بخوارزمية القوة المُفرطة (Decision Making with a Brute-Force Algorithm)
ستقوم أول خوارزمية بتطبيق حل أسلوب القوة المُفرطة الذي يعتمد على التعداد الشامل لكل الفِرق المُمكِنة وأخذها بعين الاعتبار، وستَستخدِم هذه الخوارزمية أدوات combinations (توافيق) من وحدة itertools؛ لتوليد كل الفِرق المُمكِنة ذات العدد المحدَّد.
سيتم توضيح الأداة بالمثال البسيط أدناه:

بعد ذلك، يمكِن إنشاء الدالة التالية لحل مشكلة تكوين الفريق بأسلوب القوة المُفرطة، وهذه الخوارزمية تأخذ بعين الاعتبار جميع أحجام الفِرق المُمكِنة، ويتم إنشاء الفِرق بناءً على الأعداد المُمكِنة، ثم تقوم بحصر الفِرق التي تستوفي كل المهارات المطلوبة وتحدِّد الفريق الأقل عددًا:

من الممكن ألا يكون هناك حل لنسخة المشكلة الواردة، فإذا كانت مجموعة المهارات المطلوبة تشمل مهارة لا يمتلكها أي عامل من العمَّال المتواجدين، فلن تجد طريقة لإنشاء فريق يغطي كل المهارات، وفي مثل هذه الحالات ستُظهر الخوارزمية المذكورة سابقًا النتيجة بعدم وجود حل.
بإمكانك الآن استخدام المقطع البرمجي التالي لاختبار خوارزمية الحل بالقوة المُفرطة وفقًا للمثال الذي تم إنشاؤه سابقًا:
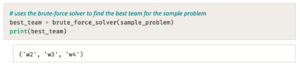
من المؤكد أن خوارزمية الحل بالقوة المُفرطة ستجد أفضل حل ممكن، أي: أقل الفِرق عددًا طالما أن هناك حل ممكِن، ولكن كما تم مناقشته في بداية هذا الموضوع فإن طبيعة الخوارزمية الشمولية تؤدي إلى زيادة هائلة في التكلفة الحاسوبية كلما زاد حجم المشكلة.
يمكِن توضيح ذلك من خلال إنشاء نُسخ لمشكلات متعدِّدة من حيث تزايد عدد العمَّال، ومن الممكن استخدام المقطع البرمجي التالي لتوليد نُسخ متنوعة من مشكلة تكوين الفريق، حيث يتنوع عدد العمَّال ليكون: 5 و10 و15 و20، ثم يتم توليد 100 نسخة بعدد العمَّال، وتشمل كل النُسخ المهارات الإجمالية العشر، والمهارات الثمان المطلوبة، والخمس مهارات كحدٍّ أقصى لكل عامل:

تَقبل الدالة التالية قائمة بنُسخ المشكلة وخوارزمية الحل بالقوة المُفرطة، ويتم استخدام هذه الخوارزمية لإجراء العمليات الحسابية ثم استخراج الحل لجميع النُسخ، كما أنها تقوم بتسجيل الوقت الإجمالي المطلوب (بالثواني) لحساب الحلول وكذلك العدد الإجمالي للنُسخ التي يُمكِن إيجاد حل منها:

مشكلة تخصيص الموارد
يَستخدِم المقطع البرمجي التالي هذه الدالة وخوارزمية الحل بالقوة المُفرطة لحساب الحلول المُمكِنة لمجموعات البيانات التي تم إنشاؤها سابقًا والمُكوَّنة من 5-workers (خمسة_عمَّال)، و10-workers (عشرة_عمَّال)، و15-workers (خمسة عشر_عاملًا)، و20-workers (عشرين_عاملًا):

على الرغم من أن الأعداد المطلوبة تم تسجيلها بواسطة الدالة gets_solutions () إلا أنها ستكون متفاوتة نظرًا للطبيعة العشوائية لمجموعات البيانات، وسيكون هناك نمطان ثابتان على الدوام هما:
- زيادة على العمَّال تؤدي إلى عدد أكبر من نُسخ المشكلات التي من الممكن إيجاد حل لها، وهذا النمط من الحلول معقول ومتوقَّع؛ لأن وجود عدد كبير من العمَّال يزيد من احتمال وجود عاملٍ واحدٍ على الأقل يمتلك مهارة واحدة مطلوبة ضمن مجموعة العمَّال المتاحة.
- زيادة عدد العمَّال يؤدي إلى زيادة كبيرة (أُسِّيَّة) في الزمن الحاسوبي، وهذا متوقع حسب التحليل الذي تم إجراؤه في بداية هذا الموضوع، وبالنسبة لمجموع العمَّال ممن هم بعدد: 5، 10، 15، 20 عاملًا، فإن عدد الفِرق المُمكِنة يساوي: 31، 1023، 32767، و1048575 على الترتيب.
بصفة عامة، وبالنظر إلى عدد العمَّال المُعطى N، فإن عدد الفِرق المُمكِنة يساوي 2N-1، وهذا العدد سيصبح كبيرًا لتقييمه حتى بالنسبة للقيم الصغيرة لـ N.
كذلك بالنسبة لأي مشكلة بسيطة بها قيد واحد (يغطي جميع المهارات المطلوبة) وهدف واحد (تقليل حجم الفريق)، فإن القوة المُفرطة قابلة للتطبيق فقط على مجموعات البيانات الصغيرة جدًا، وذلك بالتأكيد ليس حلًا علميًّا لأي من مشكلات التحسين المعقَّدة التي نواجهها في الواقع والتي أشرنا إليها في بداية الموضوع.
بإمكانك مراجعة محتوى موضوع “مشكلة تخصيص الموارد” بدايةً من عنوان “الحل الأمثل” وحتى نهاية هذا القسم، من خلال الرابط التالي:
اتخاذ القرار باستخدام خوارزمية استدلالية جشعة (Decision Making with a Greedy Heuristic Algorithms)
تتعامل الدالة التالية مع هذا القيد بواسطة تنفيذ خوارزمية تحسين تعتمد على الأسلوب الاستدلالي الجشع، حيث تقوم الخوارزمية تدريجيًّا بتكوين الفريق عن طريق إضافة عضو واحد في كل مرة، فالعضو الذي تمت إضافته مؤخرًا يكون دائمًا هو العضو الذي يمتلك معظم المهارات التي لم توجد في سابقه، وتستمر العملية حتى تستوفي جميع المهارات المطلوبة.
لاحظ أن
الدالة الاستدلالية الجشعة (Greedy Heuristic) المُستخدَمة في هذا المثال هي معيار لاختيار عامل يتوفر فيه أكبر عدد من المهارات التي تُستوفى في الفريق إلى الآن، ومن الممكن استخدام دالة استدلالية أخرى، مبنية على إضافة العامل الذي يتوفر فيه العدد الأكبر من المهارات أولًا.

مشكلة تخصيص الموارد
لا تأخذ خوارزمية الحل الجشعة كل الفِرق المُمكِنة بعين الاعتبار ولا تضمن إيجاد الحل الأمثل، ولكنها – كما هو موضَّح بالشكل التالي – أسرع بكثير من خوارزمية الحل التي تعتمد على القوة المُفرطة، ومع ذلك بإمكانها أن تُنتج حلولًا جيدة، هي في الغالب حلول مثلى، ومن المؤكَّد أن تجد هذه الطريقة حلًّا إذا كان موجود.
يَستخدِم المقطع البرمجي التالي خوارزمية الحل الجشعة لحساب حلول مجموعات البيانات: 5-workers (خمسة_عمَّال)، و10-workers (عشرة_عمَّال)، و15-workers (خمسة عشر_عاملًا)، و20-workers (عشرين_عاملًا) التي تم استخدامها سابقًا لتقييم خوارزمية الحل بالقوة المُفرطة:
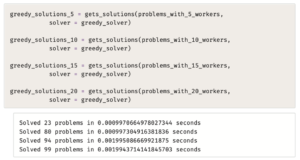
مشكلة تخصيص الموارد
والآن يتضح الفَرق في السرعة بين الخوارزميتين؛ حيث يُمكِن تطبيق خوارزمية الحل الجشعة على النُسخ المتعلقة بالمشكلات الكبيرة جدًا، كما في المثال التالي:

مقارنة الخوارزميات (Comparing the Algorithms)
بعد أن تم توضيح ميزة السرعة لخوارزمية الحل الاستدلالية الجشعة، تتمثَّل الخطوة التالية في التحقُّق من جودة الحلول التي تُنتجها، حيث تَقبل الدالة التالية الحلول التي أنتجتها الخوارزمية الجشعة وخوارزمية القوة المُفرطة على نفس مجموعة نُسخ المشكلات، ثم تبيّن النِّسب المئوية للنُسخ التي تقوم كلتا الخوارزميتين بذكر الحل الأمثل لها (الفريق الأقل عددًا):
من الممكن الآن استخدام الدالة compare () لمقارنة فاعلية الخوارزميتين المطبقتين على: الخمسة عمَّال، والعشرة عمَّال، والخمسة عشر عاملًا، والعشرين عاملًا.
توضِّح النتائج أن الخوارزمية الاستدلالية الجشعة بإمكانها أن تجد باستمرار الحل الأمثل لحوالي 80% أو أكثر من كل نُسخ المشكلات القابلة للحل.
وفي الواقع، من الممكن التحقُّق بسهولة من أن حجم الفريق الذي تُنتجه الخوارزمية الاستدلالية الجشعة حتى في النُسخ التي تفشل في إيجاد الحلول المُثلى لها يكون قريبًا جدًا من حجم أفضل فريق ممكن.
إذا تمت إضافة ذلك إلى ميزة السرعة الهائلة، تجد أن الخوارزمية الاستدلالية خيار عملي أكثر للتطبيقات الواقعية، وستكتشف في الموضوع التالي تقنيات تحسين أكثر ذكاءً، وستتعرَّف على كيفية تطبيقات على مشكلات مختلفة.
بإمكانك مراجعة محتوى موضوع “مشكلة تخصيص الموارد” بدايةً من عنوان “اتخاذ القرار باستخدام خوارزمية استدلالية جشعة” وحتى نهاية الموضوع، من خلال الرابط التالي:
إلى هنا يكون قد انتهى موضوع “مشكلة تخصيص الموارد“، لا تنسوا مراجعة نواتج التعلُّم أعلى المقال، وانتظرونا في الموضوع القادم!